Unraveling the Mystery of Your Eyeglass Prescription
What do the abbreviations OD and OS mean in an eye prescription?
The first thing to know about your eyeglass prescription is the meaning of "OD" and "OS." These abbreviations stand for oculus dexter and oculus sinister, Latin terms for "right eye" and "left eye," respectively. You may also see "OU" on your prescription, which means oculus uterque or "both eyes. It's important to note that on your prescription, the information for the right eye (OD) is listed before the left eye (OS). This is a standard practice to minimize errors, as the doctor sees your right eye on their left when facing you.
Supplemental Prescription Information
In addition to your main prescription, you'll see other terms and abbreviations. These include:
Sphere (SPH). This value, measured in diopters (D), shows the strength of the lens required to correct your vision problem. A negative diopter value indicates nearsightedness, while a positive or zero value indicates farsightedness.
The term 'spherical' refers to a lens curvature that provides equal refractive power in all meridians, correcting both nearsightedness and farsightedness.
Cylinder (CYL). This value represents the cylindrical correction required to address astigmatism. An absence of a value signifies the absence of astigmatism.
The term 'cylinder' indicates that the lens power is added asymmetrically to correct astigmatism. One meridian of the lens maintains its original curvature, while the perpendicular meridian is specifically curved to neutralize the maximum astigmatic error.
The cylinder power value in an eyeglass prescription, which may be positive or negative, is used to correct astigmatism. A negative cylinder power corrects nearsighted astigmatism, while a positive cylinder power corrects farsighted astigmatism. It's important to note that cylinder power is always listed after the sphere power in the prescription.
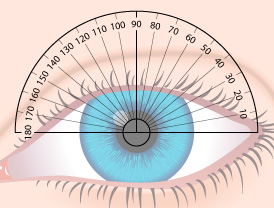
To determine the meridians of the eye, a protractor scale is placed over the front surface of the eye. The vertical line of the eye corresponds to the 90-degree meridian, and the horizontal line aligns with the 180-degree meridian.
Axis.The axis parameter denotes the meridian of the lens with zero cylindrical power, used to correct astigmatism. The axis is measured in degrees, with 90 representing the vertical meridian and 180 representing the horizontal meridian.
If a prescription includes a cylinder power value, it must also include an axis value. This axis value, which indicates the orientation of the astigmatism, is written after the cylinder power and is preceded by an 'x' when written by hand.
The axis is positioned 90 degrees from the principal meridian of the cylinder.
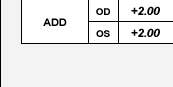
Add. This portion of the multifocal lens prescription specifies the extra magnifying power added to the lower segment of the lens to compensate for presbyopia. This power is always positive, ranging from +0.75 to +3.00 diopters, and is usually identical for both eyes.
Prism. This figure, expressed in prism diopters (p.d.), indicates the degree of prismatic correction necessary to rectify ocular misalignment. Prism is an uncommon component of eyeglass prescriptions.
Prism, if required, is indicated by its strength (in metric or fractional units like 0.5 or ½) and direction. Direction is denoted by the position of the prism's thickest edge relative to the wearer: BU (base up), BD (base down), BI (base in), or BO (base out).
Sphere power, cylinder power, and add power, all measured in diopters (D), are expressed in decimal form. These values are usually rounded to the nearest quarter-diopter (0.25 D). Axis values, ranging from 1 to 180, are whole numbers that specify a specific meridian. Prism diopters, when indicated in decimal form, typically have only one digit after the decimal point (e.g., 0.5 D).
Background
Blur, a subjective optical phenomenon, occurs when the eye cannot accurately refract light onto the retina. The severity and type of refractive error influence the extent of blur. Common examples of blurred vision due to refractive errors are:


Blurred vision can be corrected by focusing light precisely on the retina. This is often accomplished using eyeglasses or contact lenses. Alternatively, surgical procedures or specialized contact lenses can physically reshape the eye's structures to improve focus.
Eyeglasses, while primarily intended to correct refractive errors, can introduce various optical aberrations. These may include magnification, minification, distortion, chromatic aberration, and altered depth perception. It's important to note that eyeglasses primarily function to reduce blur, not to magnify objects. However, depending on the specific lens design and power, they can induce magnification or minification as a side effect.
Lens strength
The "sphere" and "cylinder" columns in an eyeglass prescription denote the refractive power of the lenses in diopters (D). A higher diopter value corresponds to a greater refractive index, and thus, a stronger lens. A diopter is defined as the reciprocal of the focal length measured in meters. Hence, a lens with a focal length of 1/3 meter has a refractive power of 3 diopters.
A lens with a +10 diopter prescription, corresponding to a 10-centimeter focal length, would serve as a suitable magnifying glass. Such a strong lens significantly magnifies objects, unlike eyeglasses, which primarily adjust the eye's focus. The natural lens within the human eye possesses a refractive power of 60 diopters.
By stacking lenses, their individual strengths are added together. For instance, a +1 diopter lens and a +2 diopter lens, when combined, form a system with a total power of +3 diopters.
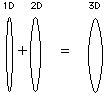
Lenses are classified by their power, which can be positive or negative. A positive lens converges light rays, making objects appear larger. Conversely, a negative lens diverges light rays, making objects appear smaller. In many cases, you can visually assess a lens's power by looking through it.
Positive refractive lenses converge light rays, including sunlight.




This series of images demonstrates the optical projection of a 1-diopter lens onto a surface at varying distances. The projected image, initially resembling the lens's physical form, becomes increasingly circular and focused as the distance increases, illustrating the principles of lens convergence.
Negative lenses diverge light rays, preventing them from converging.
When a negative lens is paired with a positive lens, the negative lens weakens the positive lens's strength. Specifically, a -2 diopter lens combined with a +5 diopter lens results in a net strength of +3 diopters.
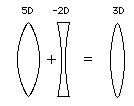
When a -3 lens and a +3 lens are placed together, their opposing optical strengths cancel each other out, leaving the combination nearly indistinguishable from a flat piece of glass.
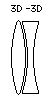
In scientific diagrams, positive lenses are shown as curved outward on both sides, while negative lenses curve inward. To achieve the best image quality, light should strike a lens at a right angle. For eyeglasses, this necessitates a meniscus shape, where the lens is curved inward toward the eye.
Lenses with spherical surfaces
Usually:
- the "spherical" component is the main correction
- the "cylindrical" component is "fine tuning."
The optical properties of lenses can be manipulated to magnify, defocus, or correct aberrations in an image.
Irrespective of the optical setup, spherical lenses exhibit isotropic behavior, impacting light rays equally in all meridians. Consequently, they induce uniform magnification, blur, or correction across all visual axes.
A spherical lens, such as a simple magnifying glass, possesses isotropic magnification properties. This implies that the lens magnifies objects equally in all directions, resulting in a uniform increase in both the vertical and horizontal dimensions of the image.

Similarly, when a spherical lens induces defocus, it results in a uniform blurring effect, affecting all orientations equally.

This kind of blur, devoid of astigmatism, results in a generalized haziness across the entire visual field.

Magnitude of refractive error and level of visual impairment
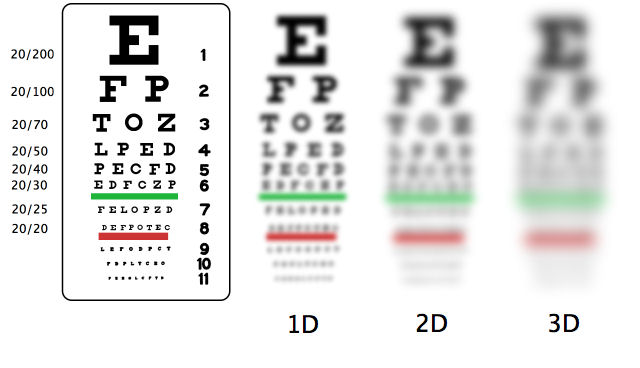
The initial image displays a Snellen eye chart as it would be perceived by an individual with normal vision or by one wearing appropriate corrective eyewear.
To provide a basic understanding of the visual impact of different levels of refractive error, images 1D, 2D, and 3D depict the approximate degree of blur that individuals with 1, 2, or 3 diopters of refractive error, respectively, might experience. For example, a nearsighted individual needing a -2.0 diopter corrective lens would visualize a standard eye chart, viewed from the standard 20-foot distance without glasses, akin to the 2D image.
As a general guideline, for every additional 0.25 to 0.5 diopters of refractive error, you might expect to lose approximately one line of vision on an eye chart.
The apex of many eye charts signifies 20/200 visual acuity, a level of sight that numerous individuals are unable to attain without the aid of corrective lenses. It is essential to understand that legal blindness is assessed based on corrected visual acuity, not uncorrected. For example, the U.S. Social Security Administration defines legal blindness as a condition wherein visual acuity cannot be enhanced beyond 20/200 in the better eye, even with the use of corrective lenses. While corrected visual acuity is paramount in numerous contexts, uncorrected visual acuity is relevant in specific circumstances, such as obtaining a driver's license without the requirement for corrective lenses. Individuals necessitating corrective lenses may still be eligible for a driver's license, but it will be contingent upon the use of such lenses while driving.
Cylindrical lenses and astigmatism correction
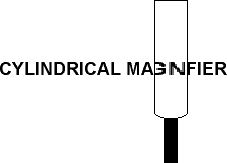
Cylindrical lenses, specialized for wide-format text magnification, function by magnifying along a single axis. This results in a one-dimensional magnification effect, as illustrated by the magnifier, which elongates characters vertically without affecting their horizontal dimension.
A cylindrical lens, unlike a spherical lens, blurs an image in a specific orientation, rather than uniformly in all directions.
This is the kind of blur that results from uncorrected astigmatism. The letters are smeared and indistinct, resembling a charcoal drawing that has been rubbed. A cylindrical lens can sharpen this kind of directional blur. When examining an eye chart, this is how the distortion might manifest:
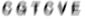
Compare it to the kind of blur that is equally blurred in all directions.

When an eye doctor measures an eye—a procedure known as refraction—usually he or she begins by finding the best spherical correction. In the event of astigmatism, the subsequent step involves the introduction of cylindrical correction to neutralize the refractive error.
Axis
Spherical lenses just have a strength, such as +1.0D, or -2.5D.
Astigmatism, however, causes a directional blur. Here are two examples of the kind of blur you get from astigmatism. The letters are blurred and smeared in a deliberate, directional manner, resembling a charcoal sketch smudged with a thumb.
A cylindrical lens of the correct curvature can correct this specific blur. The second image, being more out of focus, necessitates a stronger cylindrical lens to achieve clarity.
But notice that in addition to being smeared more, the second example is smeared out in a different direction.
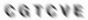
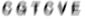
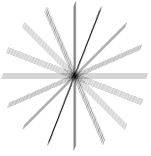
A spherical lens is identical in all directions. Its magnifying or blurring effects are consistent, no matter how you rotate it.

A cylindrical lens has both a strength and an axis. Turning it around so that the axis points in different directions changes the way it magnifies, and the way it blurs.
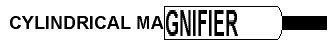
The axis specification on a prescription gives the orientation of
the axis of the cylindrical correction, and it can vary from 1 to 180
degrees:
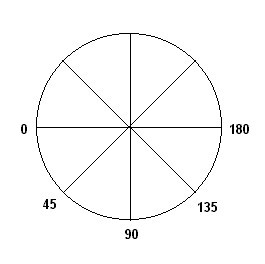
The optical power of a cylindrical lens exhibits a gradient, ranging from zero along its principal axis to a maximum at the axis perpendicular to it. Similarly, a lens with both spherical and cylindrical corrections displays varying power. Along the axis specified in the prescription, the total power equals the spherical power. However, the power increases to the sum of the spherical and cylindrical powers along the axis orthogonal to the prescribed axis.
Distance acuity and near acuity
The "DV" portion of the prescription specifies the corrective lenses required for distant vision. For individuals under forty, this typically constitutes the entire prescription. The "NV" or near-vision portion remains blank as additional correction for near vision is not necessary.
The NV portion is used in prescriptions for bifocals.
The lenses in young eyes are quite flexible, allowing them to adjust focus for objects at various distances. However, as we get older, these lenses lose their flexibility, making it harder to see things clearly up close.
This is called "presbyopia;" the "presby-" root means "old" or "elder." (It is the same root as in the words "priest" and "presbyterian".)
The hardening of the lens is a gradual process that occurs throughout life, not a sudden event in middle age. As we age, the lens continues to harden, and around the age of 40-45, this hardening reaches a point where it starts to interfere with our ability to focus on close objects, such as reading material. This is why most people need reading glasses at this age.
Due to their greater flexibility in focusing, young children frequently inspect objects by bringing them very close to their eyes, a behavior less common in adults.
This chart (which is approximate) shows that a schoolchild has over ten diopters of accommodation, while a fifty-year-old has only two. This means that a schoolchild is able to focus on an object about 10 cm. (4") from the eye, a task for which an adult needs a magnifying glass with a rated power of about 3.5X.
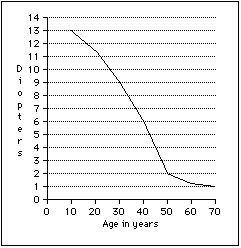
Presbyopic near vision correction can be estimated using age as the sole predictor variable. This approach offers sufficient precision for many clinical applications, particularly for low-power corrections. A specialized calculator is available for more accurate computations.
Divergences in prescription nomenclature and syntax
There exists a surprising degree of variability in the formatting and nomenclature employed in written prescriptions.
When no correction is needed, the spherical power will sometimes be written as "0.00" and sometimes as "Plano" or "Pl" because the lens, although not flat, is optically equivalent to a flat piece of glass.
When cylindrical correction is needed, the mathematics and optics of the way lenses combine mean that there are two different ways to write the same correction. One is called the plus-cylinder form and the other the minus-cylinder form. These two prescriptions are equivalent:
| Spherical | Cylindrical | Axis |
|---|---|---|
| +2.00 | +1.00 | 090 |
| +3.00 | -1.00 | 180 |
Both of them specify a power of 2.00 diopters at the 90 degree axis and 3.00 diopters at the 180 degree axis.
The first one specifies a 2.00 spherical component, which, by itself, would give a power of 2.00 diopters along both the 180 and 90 degree axis, and adds a 1.00 cylindrical component at 180 degrees (perpendicular to the axis listed on the prescription, as explained under Axis). The result is 2.00 diopters at 90 degrees and 2.00 + 1.00 = 3.00 diopters at 180 degrees.
The second specifies a 3.00 spherical component, which by itself would give a power of 3.00 diopters along both the 180 and 90 degree axis, and subtracts a 1.00 cylindrical component at 90 degrees. The result is 3.00 - 1.00 = 2.00 diopters at 90 degrees and 3.00 diopters at 180 degrees.